當需要昂貴的專家標註時，影像標註可能是機器學習應用的瓶頸。一些例子包括醫學成像、天文學或植物學。

為了緩解這個問題，小樣本分類旨在從少量（幾個）樣本（樣本）中訓練分類器。一個典型的場景是一樣本學習，每個類別只有一個影像。另一個是零樣本學習，其中類別以不同的格式提供給模型。例如，我可以告訴你“玫瑰是紅色的，天空是藍色的”，你應該能夠在沒有實際看到任何圖片的情況下對它們進行分類。

最近的研究利用未標記資料來提升小樣本效能。一些例子包括標籤傳播和嵌入傳播。這些方法屬於“轉導式”和“半監督”學習 (SSL) 類別。在這篇文章中，我將首先概述小樣本學習領域。然後，我將以標籤傳播和嵌入傳播為例解釋轉導式和 SSL。

小樣本分類

在由 Vinyals 等人 提出的典型小樣本場景中，模型會呈現由支援集和查詢集組成的情景。支援集包含有關我們想要對查詢進行分類的類別的資訊。例如，模型可以得到一張計算機和平板電腦的圖片，然後它應該能夠對這兩個類別進行分類。事實上，模型通常會得到五個類別（5 路），每個類別一個（單樣本）或五個（五樣本）影像。在訓練過程中，模型會收到這些情景，它必須學會根據支援集正確猜測查詢集的標籤。在訓練、驗證和測試期間看到的類別都是不同的。這樣，我們就可以確定模型正在學習適應任何資料，而不僅僅是記憶訓練集中的資訊。雖然大多數演算法使用情景，但不同的演算法家族在如何使用這些情景訓練模型方面有所不同。接下來，我將介紹三個演算法家族：度量學習、基於梯度的學習和遷移學習。

度量學習方法

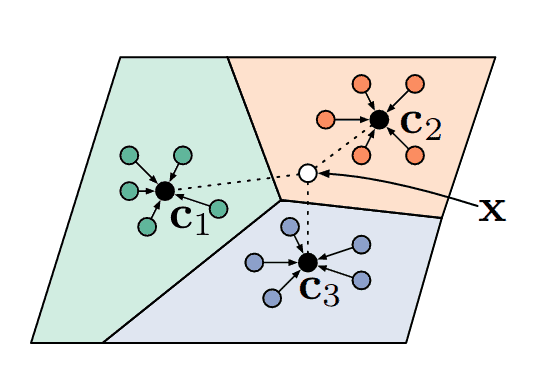
目前，小樣本學習最簡單也是最流行的方法是度量學習。在這種正規化中，模型學習將影像投影到一個空間中，在這個空間中，給定一些距離度量，相似的類別彼此靠近，而不同的類別則相距更遠。也許最著名的小樣本學習模型是k 近鄰，它會將查詢分配給與其最近的支援相同的標籤。事實上，原型網路 (Snell 等人)，目前最流行的小樣本演算法之一，就是基於相同的度量學習原理，見圖 1。

基於梯度的方法

這類演算法，例如模型無關元學習或 MAML (Finn 等人)，學習一個好的網路初始化，以便透過在給定支援集上微調模型來解決任何問題。在每次訓練迭代中，MAML 會同時最佳化網路引數的多個副本，然後透過所有這些最佳化進行反向傳播來更新原始權重。MAML 啟發了許多後來的研究，例如 Reptile、iMAML 或 ANIL。

遷移學習方法

最近，遷移學習方法已成為小樣本分類的最新技術。像無遺忘動態小樣本視覺學習 (Gidaris & Komodakis) 這樣的方法在第一階段預訓練一個特徵提取器，然後在第二階段，它們學習重用這些知識以在新的樣本上獲得一個分類器。由於其成功和簡單性，遷移學習方法在兩篇最近的論文 (Chen 等人、Dhillon 等人) 中被稱為“基準”。

不用說，還有很多沒有在這裡引用但值得花時間的工作，以及貝葉斯或生成方法。但是，這篇文章的目的是介紹轉導式小樣本學習，它是在簡要介紹小樣本學習之後進行的。

轉導式小樣本學習

機器學習中最常見的分類場景是歸納式場景（或者說不是這樣，正如你將要看到的那樣…）。在這種情況下，我們必須學習一個函式，該函式為任何給定輸入生成一個標籤。與之不同的是，在轉導式場景中，模型可以訪問我們想要分類的所有未標記資料，它只需要為這些樣本生成標籤（而不是為所有可能的輸入樣本生成標籤）。在實踐中，轉導被用作一種半監督學習形式，其中我們有一些未標記的樣本，模型可以從這些樣本中獲得有關資料分佈的額外資訊以進行更準確的預測。在小樣本學習中，轉導式演算法會利用情景中的所有查詢，而不是將它們單獨處理。對這種場景的一種可能的批評是，每個類別通常有 15 個查詢，而且在現實生活中獲取平衡的未標記資料是不現實的。正如 Nichol 等人 在他們的論文中指出的那樣，請注意，由於批歸一化，許多小樣本演算法已經是轉導式的。

最近，由於 Liu 等人 的工作，轉導式演算法在小樣本分類中越來越受歡迎。他們利用了一種名為標籤傳播的轉導式演算法。那麼，標籤傳播是什麼呢？

標籤傳播

標籤傳播 (Zhu & Ghahramani) 是一種演算法，它透過圖的節點傳遞標籤資訊，其中節點對應於標記和未標記的樣本。該圖是基於嵌入之間的一些相似性度量構建的，因此圖中彼此靠近的節點被認為具有相似的標籤。與其他演算法（例如 KNN）相比，其主要優勢在於標籤傳播尊重資料的結構。以下是我做的一個例子

雖然這種傳播演算法是迭代的，但 (Zhou 等人) 提出了一個封閉形式的解決方案。該演算法如下所示

2. 然後計算 $S=D^{-\frac{1}{2}}WD^{-\frac{1}{2}}$ 拉普拉斯矩陣，它可以被看作是圖的矩陣表示。

3. 獲取傳播器矩陣 $P=(I-\alpha S)^{-1}$。基本上，這個矩陣告訴你從一個節點到另一個節點需要傳遞多少標籤資訊。

4. 最後，給定一個矩陣 $Y$，其中每一行都是節點的獨熱編碼，大多數行都是由 0 組成（未標記的樣本），而一些行在相應的類別中包含一個 1，則最終標籤 $\hat{Y}$ 為 $PY$。

矩陣求逆是一個昂貴的操作，這使得它難以應用於大型資料集，但幸運的是，小樣本情景很小。因此，Liu 等人 提出了一個用於小樣本學習的轉導式傳播網路 (TPN)，如以下圖所示

這個想法是，支援集的標籤透過圖傳播到查詢集。這種架構被證明非常有效，獲得了最先進的結果，並啟發了新的最先進方法，例如嵌入傳播。

嵌入傳播

正如 Chapelle 等人 解釋的那樣，半監督學習和轉導式學習演算法對資料做出了三個重要假設：平滑性、聚類和流形假設。在最近的 嵌入傳播 論文（發表於 ECCV2020）中，作者基於第一個假設來改進轉導式小樣本學習。具體來說，這個假設說，在嵌入空間中彼此靠近的點在標籤空間中也必須彼此靠近（相似的點具有相似的標籤）。為了實現這種平滑性，作者應用標籤傳播演算法來傳播影像特徵資訊，而不是像你在下圖中看到的那樣傳播標籤資訊

這意味著彼此相似的節點會變得更加靠近，從而提高嵌入空間的密度。因此，應用於這些新的密集嵌入的標籤傳播會獲得更高的效能

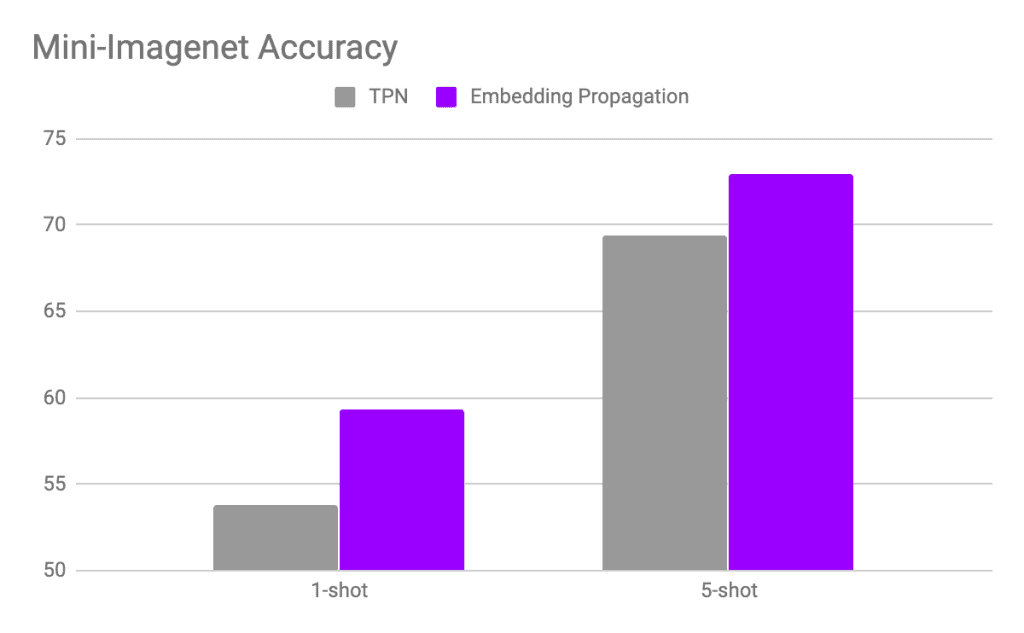
此外，作者表明他們的方法對半監督學習和其他轉導演算法也有益。例如，他們將嵌入傳播應用於Gidaris 等人提出的少樣本演算法，平均效能提高了 2%。作者在他們的github 儲存庫中提供了 PyTorch 程式碼。您只需新增 3 行程式碼即可在您的模型中使用它。

import torch
from embedding_propagation import EmbeddingPropagation

ep = EmbeddingPropagation()
features = torch.randn(32, 32)
embeddings = ep(features)

結論

轉導學習已成為少樣本分類中的一個反覆出現的主題。在這裡，我們看到了什麼是轉導學習以及它如何提高少樣本演算法的效能。我們還看到了它的一些缺點，例如未標記資料的平衡假設。最後，我解釋了最近的嵌入傳播演算法來改進轉導少樣本分類，並給出了關於它為何有效的一些直覺。